하느님 께서 아이들이 암에 걸리도록 허용하실까요? 아마도...
시험 결승전에서 수학 문제에 대한 카르마 군의 답을 이해하려고 노력하고 있습니다.
문제에 대한 참조와 설명을 검색했지만 아무 소용이 없습니다. 나는 여전히 문제에 대한 끔찍한 설명을 이해할 수 없었고 대답은 당신이 그들의 사고 과정을 알고 있다고 가정합니다.
이 문제에 대한 영어 번역이 있습니다.
young-il-long-kiyoshi.tumblr.com/post/125623681248/on-the-topic-of-the-final-maths-question-in-the
문제를 언급했지만 설명하지 않은 또 다른 링크.
angryanimebitches.com/2016/03/assassination-classroom-season-2-episode-12-the-principal-is-a-sore-loser/
그들은 또한 Karma-kun의 대답을 설명하는 유튜브 비디오이지만 그의 설명조차도 그가 중심 원자의 면적이 입방체 면적의 절반을 2로 나눈 것과 같다는 결론을 어떻게 이해하지 못합니다. a ^ 3 / 2
비디오 링크 : 이상한 기하학 (암살 교실 S2 E12)
내가 이것을 게시하는 이유는 스레드에서 묻지 않고 문제를 이해할 수있는 다른 방법이 없기 때문입니다.
전문 박사 수준이 아닌 "고등학교"수준의 관점에서 답변에 대한 설명을 원합니다.
"등거리", "최소한", "정점"또는 내가 이해할 수없는 다른 기술 용어를 듣고 싶지 않습니다.
내가 너무 많은 것을 요구한다는 것을 알고 있지만 Karma-kun이 어떻게 얻었는지 이해하도록 도와주세요. a ^ 3 / 2. 내가 카르마에서 얻은 유일한 관점은 8 개의 원자가 모두 자신의 입방체를 형성하고 그 상상의 입방체의 중간 점은 8 개의 개별 입방체 안에있는 모든 원자와 동일하다는 것입니다.
그리고 비디오도 그렇게 말합니다.하지만 어떻게 세상에서 1/8 ...에 2A? 그리고 a ^ 3 / 2
여기에 표시된대로 :
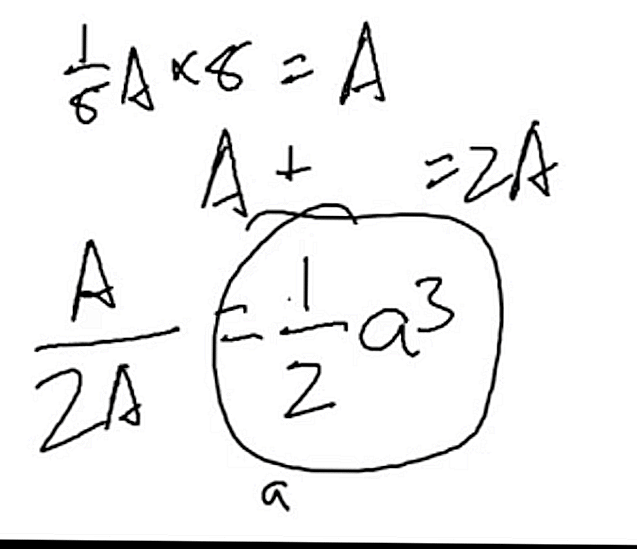
- 아사노 군의 해결 방법은? math.stackexchange.com/questions/3193480/…
결정 격자의 모든 원자는 동일합니다. 꼭지점에있는 원자의 부피 (모퉁이가 아니라 모서리 인 경우 약간 다른 추론이 필요함)가 B라고합시다. 꼭지점에있는 각 원자는 큐브의 (1/8) B를 차지합니다. 다이어그램을 참조하십시오.
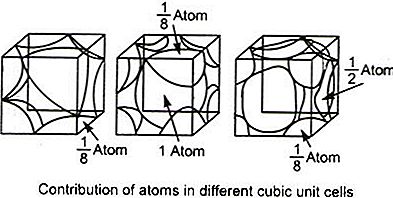
길이가 a 인 큐브의 경우, 볼륨 D를 갖는 중심 원자 A와 큐브의 (1/8) B를 차지하는 정점에있는 8 개의 원자로 구성됩니다. 그러므로,
ㅏ3 = D + 8 × (1/8) B
그러나 우리는 꼭지점의 원자가 실제로 중심 원자와 동일하다는 것을 알고 있기 때문에 부피 B는 D와 같으므로
ㅏ3 = B + 8 × (1/8) B ==> B = (1/2) a3
QED
말씀하신 모든 전문 용어는 제가 고등학교에서 배웠던 것입니다. Karma가 말했듯이이 질문은 어렵지 않습니다. 수학과 화학의 결합 된 문제입니다.
7- 1하지만 여기가 아닌 수학 포럼에서 질문해야한다고 생각합니다. 어색해 보인다.
- 하지만 왜 2 이상 공식 a ^ 3 / 2 ??
- 여기서 2 이상은 입방체의 경우 부피의 절반 만 특정 원자 A가 차지하는 부피이고 나머지 부피는 다른 원자가 공유한다는 것을 알려줍니다.
- 그러니 내가 당신을 제대로 따르고 있다면 A / 8 * 8 = A, 8 개의 꼭지점이 원자 2 개를 차지합니다. 2A. 그 이후로 ㅏ 큐브의 절반입니다. A / 2A... 그리고 원자의 부피를 계산하기 위해 우리는 x, y, z 그것은 3D 그리고 우리는 큐브의 면적을 찾는 공식으로 끝납니다. a ^ 3 권리? 그럼 우리는 반으로 2 이상? a ^ 3 / 2
- 아니요, 꼭지점에있는 8 개의 원자는 입방체에서 하나의 원자 공간을 차지합니다. A / 2A는 중심 원자가 차지하는 부피 대 중심 원자와 꼭지점의 원자를 구성하는 총 부피의 비율을 찾는 데 사용됩니다. 그래서 우리는 원자 A가 입방체 부피의 1/2을 차지하고 따라서 a ^ 3 / 2를 차지한다는 것을 압니다.
이 질문에 늦었다는 것을 알고 있지만 여기에 아마도 더 간단한 설명이 있습니다. 나는 방금 애니메이션 에서이 문제에 도달했고 그들이 대답을 밝히기 전에 그것을 해결하고 싶었습니다.
확인. 중간에 원자가있는 입방체가 있습니다. 당신이하고 싶은 것은 큐브를 여덟 조각으로 나누는 것입니다. 이 조각들 중 하나를 가져 가십시오. 반대쪽 모서리 (정점)에는 두 개의 원자가 있습니다. 이들 원자 중 하나는 중심 원자 [A] 0이고 다른 하나는 가장자리의 원자입니다. 이 8 분의 1 입방체의 정확히 절반이 다른 원자보다 한 원자에 더 가깝다는 것은 단순한 논리로 진행됩니다. 이것은 다른 8 개 조각에 적용되므로 중심 원자에 가까운 입방체의 부피는 단순히 전체 부피의 절반입니다.
문제는 보이는 것보다 훨씬 간단하며 내가 멍청하다는 것을 깨닫기 전에 기하학적 조각으로 볼륨을 계산한다는 것을 인정합니다. 많은 수학이 필요하지 않습니다. 논리에 대한 확실한 이해와 약간의 영리함.
아마도 만화의 대답 자체는 정확하지 않습니다. 원자가 각 입방체 내에서 같은 양의 공간을 차지하면 (a)의 절반이됩니다-보이지 않는 선). 당신은 본질적으로 그것을 3의 파이 곱하기 r의 제곱 인 3의 3 배인 구체의 부피를 풀기위한 공식에 대입 할 수 있습니다.이 경우, 당신의 r (반지름)은 a / 2입니다. 따라서 하나의 원자가 보이지 않는 선의 절반을 차지합니다)
기본적으로 V = 4 / 3 * π * (a / 2) ^ 3
V = 4 / 3 * π * a ^ 3 / 8
V = 4 (4/3에서)는 8 (in a ^ 3 / 8)을 취소하므로 1 / 3 * π * a ^ 3 / 2를 얻습니다.
V = π * a ^ 3 / 6
기타 : * = 시간, ^ = 거듭 제곱, π = 파이.